Explorer 1 said:

"A 2D map of C-G seems like a tough order; the projection math alone..."


Don't worry! If you can put a grid on the surface (as we have seen already), you can warp that grid into any map projection you like. Mapping will be no huge problem - in fact I expect they have a rough one already (I've been playing with one myself).

Phil

It would appear that the neck is an "erosional" feature (not sure if erosion is the right word), and maybe not the contact boundary between 2 separate bodies. At some point in the future, the neck will sublime away and the comet will split in two.

Gravity must be very low there, caught as it is between two lumps o' rock. A higher chance for material to be lost, maybe?

Andy

Interesting though that a unique coordinate system (projection) is possible as seen in the rotating map. None of the overhangs appear to wrap back on themselves as seen from the central projection point. Thus a 2D map should be possible with access to the shape model (as Phil alluded to earlier).

I concur, not that we have a final word yet but I do tend to think the shape is from melting and erosion, rather than 2 objects that have merged since that is a less likely scenario.

@AndyG: Gravity is nearly negligible, gas pressure define this environment with sublimation and active geysers, though I wonder if the latter could create a static charge.

That's possible with any simply connected object (no "handle-shaped holes") in 3d via a homeomorphism (continuous map).
For objects with holes, like doughnuts different coordinate systems are needed. The shape of the nucleus is strange, but fortunately not that strange.

Sounds good, though it seems to me that C-G would be more straightforward than some other simply connected objects. A latitude/longitude with respect to C-Gs center of gravity appears to be possible as a "planetocentric" or "cometocentric" coordinate. It would be a simple tracing of rays emanating from the central point and then intersecting the surface. Each ray has just a single intersection with the surface.

As long as there are no relevant overhangs (in the sense of the rays). I'm not quite sure whether this holds for the comet.
It could become a little more tricky.

Good point. A closer look at the recent animation shows a few localized breaks in the grid lines. This correlates with some local topography that has addtional intersection points with the rays pointing at the center of gravity. Perhaps one would have to filter out these bumps in a shape model to come up with a reference shape that could be specified using a cometocentric coordinate. Then the actual surface can be compared with normals to this reference shape.

Eyewitnessing it will be simply amazing.
On the opposite side, mapping an evolving body will be a pain!

Not a pain, it just means the cartographers have long-term employment!

Phil

Wouldn't the two lobes just gradually come back together together as the neck erodes, if their mass remains the same? Unless a decrease in radius forces C-G to rotate faster and faster (I guess we'll find out soon!)

I think you're right, the lobes would collapse together as the neck was eroded.

Phil

I believe the centrifugal forces at the rotational rate of ~ 1 revolution per day are stronger than the combined gravitational attraction of the two lobes. If the neck breaks they would come apart, as I see it. Would be interesting to see calculations of the eventuality.

Rotation rate is 12.7 hours. The circumference drawn by the 4km length of the comet ( a 2km radius ) is 12.6 km

So very roughly - it's doing 1km/hr or 0.28m/sec. V^2/r is thus 0.000039 m/sec^2

Surface gravity is approximated as 10^-3 m/sec^2 3 orders of magnitude higher than the centripetal acceleration due to rotation.

Thus no - they would not fly apart. They would collapse together.

The key variable between these scenarios is mass, which will presumably be known in time to a high degree of precision. (Probably not nearly as soon as it would be for a symmetrical body; Rosetta's navigators are probably gonna have an interesting time for quite a few orbits until they get a handle on the mass distribution of C-G).

EDIT: Whups, cancel that. What Doug said. Obviously the system's mass is constrained well within an order of magnitude already.

Every irregular object eroded from the outside must eventually form a neck which breaks and the two parts will settle together, tumbled or not. How would they get the energy to fly apart again?

Could acquire more angular momentum from impacts over time; then the variable would become the shear strength of the 'neck'. But as Doug observed, it's not spinning fast enough.

If it were rotating fast enough to displace the two halves if the 'neck' were to disappear....then it would also be rotating fast enough to rip itself to shreds.

What I have in essence done is prove that the comet can exist (which is somewhat self evident)

I'm not convinced by the emerging consensus that the neck is an erosional feature. It seems to me that the neck is near a gravitational low (i.e., "downhill" from the rest of the comet) and any loose material near the comet would be likely to settle there.

In previous passes by the Sun the comet would eject both volatile gases and particles of solids; some of them might not achieve escape velocity. The volatiles would be reheated on the surface and escape again but we would expect the solids to settle back in the lowest point, the comet's neck. This model predicts a dustier area near the neck with a comparatively lower concentration of volatiles.

We'll see what turns up but I'm not a geologist so what do I know.

Steve M

It's where the bulk of activity appears to be
http://sci.esa.int/rosetta/54471-comet-act...-2-august-2014/

No - the centripetal acceleration is 4 orders of magnitude less than the escape velocity.

Back of the envelope:
Gravity /centripetal ~ GM/r^2//V^2/r ~ GpP^2 where G = grav constant of 6.67x 10^-11 (mks), p = density ~ 10^3 (mks) and P = period ~4.6x10^4 sec.
Ratio ~ 10^2
Gravity wins hands down. Tidal forces are insufficient.
Adjustments to Fg due to odd shape may cause ratio be somewhat less, but increasing density will go the other way.

there is a 3d mesh ( low-res) for gaspra
http://forum.celestialmatters.org/viewtopi...p?f=4&t=636

my g-drive link to the mesh
https://drive.google.com/file/d/0B6ZYAd08tZ...dit?usp=sharing


well for 67P a Simplecylindrical map is " out the window"
the vid on youtube looks to be using a Simplecylindrical map
https://www.youtube.com/watch?v=CNGu7KbXzOs
you can tell by the STRETCHED green dots that look like lines

But a "cubemap " would work fairly well

I had been curious about the gravity field so was googling about... this poster shows some of the weirdness of "which way is up" in a simplified contact binary scenario. It makes perfect sense, but I never considered that there could be the equivalent of Lagrange points near these bodies. Close-in "orbits" would certainly not be circular, even halos are possible. And the details near the neck... hard to know.

http://www.lr.tudelft.nl/fileadmin/Faculte...nglang_Feng.pdf
snip:
Click to view attachment

According to my calculations gravity/centripetal ratio for r=2000 m and v_rot=0.28 m/s is G/a=0.0143*Ro (density)
Comets could be very fluffy so density can be between 100 to 1400 kg/m³.
Ratio is then 1.5 to 20× (not ~100 or ~1000).

This would be bad for Philae, so I've looked, where the discrepancy may come from.
One reason is -- if I calculated correctly -- a factor of 1 / 3π for the density calculation in the spherical case.
The other one is the estimated density, which has been estimated as 10^2 kg/m³.
Together we get a discrepancy factor of 30π, about 94.
Now add the non-spherical shape, and things are open again.

-- This shows, how important the ongoing gravimetric measurements are.

OK, here is visualization from Celestia. I made model in Blender, texture is from Itokawa, orbital data from SPK/BSP od NAIF NASA/JPL

http://www.youtube.com/watch?v=kETzagV37ig

For 67P/C-G, and similarly asymmetric bodies, I'd suggest a projection on an appropriate gravitationally equipotential surface, either respecting the centrifugal forces, or using the body at rest.
"Appropriate" means, the average height of the topography over the equipotential surface should be zero, if possible. As a constraint a surface should be taken, which consists of one component without singularities (and without overlapping itself, which is probably a corollary).
Projections go along the field lines of gravity.
The result is still a non-planar map.
This could be projected in a second step to planar tiles/stripes (mercator-like in a very general sense) by constraining the intrinsic curvature.
The width of the stripes would vary because of the varying intrinsic curvature.

... just to close this gap preliminarily, until an official decision is made.

thanks, Gerald, for your insights. I noticed you follow the Rosetta blog, too. Unless another Gerald is at work there! My own name (Peter Groeneweg) is a bit too difficult so on the ESA blogs I'm PeterG.

In my previous entry my use of the English language is perhaps "difficult" too, so let me say here what I really wanted to say: I feel privileged to be a member, a junior member to be more precise, of a forum that has experts like Phil in its ranks. No unmanned spaceflight subject seems too arcane for the forum!

A further thought: is a cartography system the province of ESA, or does it need endorsement by the international organization(s)? One thing seems sure: after the initial spectacular success at 67P/C-G I expect more missions to follow and a sound cartography system seems most useful to have by then.

Why along the field lines (and with respect to an equipotential surface)? That would rely to some extent on knowledge of the internal mass distribution, which may be significantly nonuniform, and at the very least would require nontrivial numerical modelling to determine. It would strike me as a good property of a projection to depend only on the geometry of the body's surface.

But all of this is probably moot since such bodies have been mapped in the past. In practice, I'd guess the projection would be tailored to the body, since some projections may not work for bodies when the surface "folds back on itself".

I admit, I couldn't help to extend the funny metaphorical thought experiment about the Philae descent and landing (with limited type setting options).
But names don't need to be unique, necessarily.


Because it corresponds to the intuitive and physical concept of "up" and "down".
Notions like slope / steepness, depression, hill, etc. make a sense. It's kind of generalization we are used to from Earth on a physical basis, not merely geometric.

Technical difficulties to find the field of gravity are going to be reduced by the orbital measurements. These measurements allow even to determine the interior mass distribution to some degree. But an estimation would do the job, too.

The surface shouldn't fold back to itself (conjectural to some degree at this point), since the gravitational potential should be defined uniquely, at least for the non-rotating body.
The body itself may be layered or contain overhangs, of course.

The up and down can be incorporated into topography by mapping height (and slope etc.) relative to the equipotential surface (with or without rotational accelerations included - with them, it corresponds to what Peter Thomas has called Dynamic Topography) - there's a literature on this especially by Peter Thomas and colleagues.

There is no one best way to map a non-spherical object, just as there is not for a sphere. In fact, we need lots of maps in different projections, and using different versions of the shape, to explore the range of possibilities, most of which few people have ever thought about in detail. For instance, the shape model used to establish locations and drive the projection might be any of these:

True topographic shape
Equipotential surface
Convex hull
Triaxial Ellipsoid (best fit)
Sphere
- also other possible shapes such as a cylinder could be considered, especially for more elongated objects.

For anything but the first, the actual surface would be projected onto the shape model along radii or surface normals (body or model), then that shape drives the map projection.

Although simple cylindrical maps contain severe distortions they are very useful as intermediate steps in mapping and they are easy to import into many mapping and visualization systems. My Itokawa mosaic, for instance, includes many distortions and one small area where the mosaic is not unique (radii exit the surface and reconnect with it, as we may see at 67P as well. But there are ways to cope with these issues and you have to start somewhere.

"A further thought: is a cartography system the province of ESA, or does it need endorsement by the international organization(s)? One thing seems sure: after the initial spectacular success at 67P/C-G I expect more missions to follow and a sound cartography system seems most useful to have by then."

ESA can choose its own method of mapping, no international agency has any role in it except the IAU Working Group for cartographic coordinates and rotational elements - the coordinate system should conform to their guidelines. But mapping - no. The field is still very immature and no standards exist, nor should they until we have much more experience with different methods.

Phil

the problem at this time is we do not have a mesh to work with
-- yes one could use "Blender" and hand carve a cube into something that looks like it

now a cube map has advantages ( sometimes) for some shapes

a hi-passed map for a mesh of Vesta ( old map 2006 data) in a uv mapped cubemap
( from a normal by Chris Laurel)
north,90 to180,0 to 90,
-90 to 0,-180to -90, south


the new DEM hi passed for comparison
-- in Simple Cylindrical projection


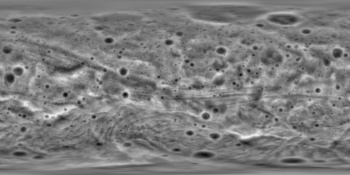
now vesta is a bad example it is rather spherical ( i just happen to be working on this asteroid right now)

so for 67p a SimpleCyl. map will not work well . BUT it is a good intermediate format and so is sinusoidal

Actually, the neck is not near a gravitational low. If you could hollow out a little sphere at where the center of mass is for the comet, at that point there'd be no gravity since the mass would be pulling from all directions equally. That's somewhere near the neck. Taking off and flying away from the neck perpendicular to the main axis is probably the lowest energy trajectory for departing (now I'm guessing).

Are these not contradictory statements?

I think there is confusion here between the scalar quantity gravitational potential and its gradient, gravitational field strength. The centre of the Earth, for example, is a low point in the gravitational potential. If you could dig a tunnel all the way there objects would certainly fall down it, even though on arrival they would have zero weight.

If you take a binary of two spherical bodies, the center of mass is in the middle of the line between those two bodies, but that's no gravitational low; it's more like a saddle; and it's a Lagrangian point (L1) at the same time, although the center of mass of two bodies doesn't need to be a Lagrangian point, in general. There are two lows at the respective centers of the two bodies.

For 67P/C-G there may also be two (or more) local gravitational lows, the deeper one near the center of the larger component.
The center of mass should be between the gravitational low of the larger component and the neck.
The neck should be near a Lagrangian point (a saddle in the field of gravity), which is between the local gravitational low of the smaller component and the center of mass.
At the center of mass there should be a net gravitational pull towards the local gravitational low of the larger component.

The center of mass is a point on the rotation axis.

Start with the Earth-Moon system as an easier-to-understand example, when reading the second paragraph a second time.

Not contradictory, more like a non sequitur.

That's what I meant to express. A small perturbation from the saddle point not exactly on the upward isoline and its downhill to one of the two lobes.

So escape velocity from the saddle point is likely lowest for the comet and it would dissipate at a higher rate, and any spray that doesn't make it off the comet from the neck is likely pulled to one of the lobes, adding to the saddle-ness of the saddle point. So for an asymetrical body, it seems that process is unstable and the asymmetry would grow, i.e., more necking.

There's probably an unstable process between the two lobes too, with one having a higher rate of dissipation and the heavier one stealing some of the lighter one's mass. But this is more guessing on my part.

That's really hard to tell at the moment, since the local gravitational lows are probably within the nucleus. Since the surface of the larger component is farther away from its local gravitational low than the surface of the neck is away from the line between the two(?) gravitational lows, we've two opposite effects which may or may not cancel out.

But I share the impression, that the surface of the nucleus isn't in perfect equilibrium between the several forces (gravity, inertial pseudo-forces, friction).
If there is some mass waste from the neck or from the smaller component towards the larger one, the field of gravity, and the rotation also change. Asymmetric loss of volatiles may change the angular velocity too.
This might eventually lead to ejection or collapse of some parts. As the comet gets closer to the Sun, I'd guess, we may see some dynamics.

I really don't think that's true. Consider a body consisting of two perfect touching spheres. Place a small test sphere on the surface of one of them and where would it roll to? Towards the contact point for sure as that is the point of lowest potential on the surface of the body. Thus the neck would tend to grow thicker.

It would do that only because it is constrained to roll on the surface of the two spheres.

Ok... I have been taking some time out from what I should really be doing - finishing a book (Emily will understand this) - to play around with some ideas about what a map of 'the nucleus that dare not speak its name' should look like.

Let me preface this by saying - this is a horrible map, very distorted and inaccurate, and the Rosetta team will do much better soon and completely discredit me. This is only intended to illustrate roughly what a proper map might look like. It's cylindrical, so the projection is very distorted to begin with.

We had a video of a shape with a lat-long grid, so that forms the basis of my coordinate system. I took images from orientations which roughly matched frames from the video and overlaid them. Two sources of error immediately - the shape was based on low res images and will not fit high res images very well to begin with, and the overlay is only approximate due to different view directions, so it's hard to match positions properly. Then I copied areas grid cell by grid cell and pasted them and distorted them to fit the grid. Lots of problems and bad fits especially in the neck area, obviously.

The grid is spaced at 15 degrees like the shape model video grid. Longitude 180 is in the middle. A separate version is annotated to show where the main features are.

Phil

Click to view attachment

Click to view attachment

Very impressive! The axis must be tilted quite a lot; given the length of the seasons it might be a very long time until much of the 'southern hemisphere' is in sunlight to fill in the black spaces.

I have seen members here mention generating synthetic "in-between" frames from two images, so this is a callout for someone to hopefully generate a bunch of frames between the two fantastic OSIRIS images that made up that 3D view: http://blogs.esa.int/rosetta/2014/08/14/comet-67pc-g-in-3d/

The generated frames could be used to create a more "comfortable" anaglyph, or even an animation of the comet's rotation.

Thanks for the map, Phil.

What about the idea to split the map into two part: one map for the potatoe shaped head, and one map for the body of the comet? On both maps there would be a circular black shape where the both are connected (the Neck).

That same idea occurred to me: map them separately as if they were Pluto and Charon, only in contact. Each part approximates a spheroid well enough. Making the common rotation axis the lynch-pin of the coordinate system forces horrendous distortions on the map. Furthermore any advantage in doing so will most likely prove ephemeral when the rotation axis shifts due to mass wasting at perihelion.

In fact the two parts may roll a bit and settle together differently at that time. How fares the coordinate system then?

this gif animation ( pre orbit data )
http://scitechdaily.com/images/New-3D-View...setta-Comet.gif

I have been able to get a ??? fair pointcloud out of the gif
-- view in meshlab


that is then meshed - in meshlab and cleaned up in blender


a link to a zip on my g-drive
67p.8-21-2014Mesh.zip - 1.8 meg with a 4k texture
https://googledrive.com/host/0B6ZYAd08tZL-V...21-2014Mesh.zip

Re - mapping the lobes separately - it's an interesting idea and I would welcome any efforts along those lines. As I said in an earlier post, there's no one best way to do it, and we need many efforts to tackle this problem in different ways. But right now I think we should wait for a more detailed shape model and more images.

Phil